Skip to content

Community detection of the countries of the world with Neo4j Graph Data Science

WRITTEN BY

Written Tomaz Bratanic

While I was waiting for my sourdough to rise, I thought, the best way to spend my time is to perform a network analysis with the Neo4j Graph data science library. Well, maybe also try to draw an acrylic painting, but I won’t bore you with that. If this is the first time you have heard of the GDS library, I can recommend some of my previous blog posts that try to explain the basics:

If you are ready, it’s time to put on our graph data science hat and get down to business.

Requirements:

Graph schema

We will be using the Countries of the world dataset made available on Kaggle by Fernando Lasso. Looking at the acknowledgements, the data originates from the CIA’s World Factbook. Unfortunately, the contributor did not provide the year the dataset was compiled. My guess is the year 2013, but I might be wrong. The dataset contains various metrics like area size, population, infant mortality, and more about 227 countries of the world.

Graph schema

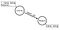
The graph schema consists of nodes labeled Country that have their features stored as properties. A Country is also a part of a Region.

Graph import

First, we need to download the dataset and copy it to the $Neo4j/importfolder. For some reason, the numbers in the CSV file use a comma as a floating point instead of a dot (0,1 instead of 0.1). We need to preprocess the data to be able to cast the numbers to float in Neo4j. With the help of an APOC procedure apoc.cypher.run , we can preprocess and store the data in a single cypher query. apoc.cypher.run allows us to run independent subqueries within the main cypher query and is excellent for various use cases.

LOAD CSV WITH HEADERS FROM "file:///countries%20of%20the%20world.csv" as row
// cleanup the data and replace comma floating point with a dot
CALL apoc.cypher.run(
    "UNWIND keys($row) as key 
     WITH row,
          key,
          toFloat(replace(row[key],',','.')) as clean_value
          // exclude string properties
          WHERE NOT key in ['Country','Region'] 
          RETURN collect([key,clean_value]) as keys", 
     {row:row}) YIELD value
MERGE (c:Country{name:trim(row.Country)})
SET c+= apoc.map.fromPairs(value.keys)
MERGE (r:Region{name:trim(row.Region)})
MERGE (c)-[:PART_OF]->(r)

Identify missing values

Another useful APOC procedure is apoc.meta.nodeTypeProperties. With it, we can examine the node property schema of the graph. We will use it to identify how many missing values each feature of the country has.

// Only look at properties of nodes labeled "Country"
CALL apoc.meta.nodeTypeProperties({labels:['Country']})
YIELD propertyName, propertyObservations, totalObservations
RETURN propertyName,
       (totalObservations - propertyObservations) as missing_value,
       (totalObservations - propertyObservations) / toFloat(totalObservations) as pct_missing_value
ORDER BY pct_missing_value DESC LIMIT 10

Results

It looks like we don’t have many missing values. However, we will disregard features with more than four missing values from our further analysis for the sake of simplicity.

High correlation filter

High correlation filter is a simple data dimensionality reduction technique. Features with high correlation are likely to carry similar information and are more linearly dependant. Using multiple features with related information can bring down the performance of various models and can be avoided by dropping one of the two correlating features.

// Only look at properties of nodes labeled "Country"
CALL apoc.meta.nodeTypeProperties({labels:['Country']})
YIELD propertyName, propertyObservations, totalObservations
WITH propertyName,
       (totalObservations - propertyObservations) as missing_value// filter our features with more than 5 missing values
WHERE missing_value < 5 AND propertyName <> 'name'
WITH collect(propertyName) as features
MATCH (c:Country)
UNWIND features as feature
UNWIND features as compare_feature
WITH feature,
     compare_feature,
     collect(coalesce(c[feature],0)) as vector_1,
     collect(coalesce(c[compare_feature],0)) as vector_2
// avoid comparing with a feature with itself
WHERE feature < compare_feature
RETURN feature,
       compare_feature,
       gds.alpha.similarity.pearson(vector_1, vector_2) AS correlation
ORDER BY correlation DESC LIMIT 10

Results:

Interesting to see that birth rate and infant mortality are very correlated. The death rate is also quite correlated with infant mortality, so we will drop the birth and death rate but keep the infant mortality. The number of phones and net migration seems to be correlated with the GDP. We will drop them both as well and keep the GDP. We will also cut the population and retain both the area and population density, which carry similar information.

Feature statistics

At this point, we are left with eight features. We will examine their distributions with the apoc.agg.statistics function. It calculates numeric statistics such as minimum, maximum, and percentile ranks for a collection of values.

// define excluded features
WITH ['name', 
      'Deathrate', 
      'Birthrate',
      'Phones (per 1000)',
      'Net migration', 
      'Population'] as excluded_features
CALL apoc.meta.nodeTypeProperties({labels:['Country']})
YIELD propertyName, propertyObservations, totalObservations
WITH propertyName,
       (totalObservations - propertyObservations) as missing_value
WHERE missing_value < 5 AND 
      NOT propertyName in excluded_features
// Reduce to a single row
WITH collect(propertyName) as potential_features
MATCH (c:Country)
UNWIND potential_features as potential_feature
WITH potential_feature, 
     apoc.agg.statistics(c[potential_feature],
                        [0.5,0.75,0.9,0.95,0.99]) as stats
RETURN potential_feature, 
       apoc.math.round(stats.min,2) as min, 
       apoc.math.round(stats.max,2) as max, 
       apoc.math.round(stats.mean,2) as mean, 
       apoc.math.round(stats.stdev,2) as stdev,
       apoc.math.round(stats.`0.5`,2) as p50,
       apoc.math.round(stats.`0.75`,2) as p75,
       apoc.math.round(stats.`0.95`,2) as p95,
       apoc.math.round(stats.`0.99`,2) as p99

Results

The Federated state of Micronesia has the ratio of coast to area at 870, which is pretty impressive. On the other hand, there are a total of 44 countries in the world with zero coastlines. Another fun fact is that Greenland has a population density rounded to 0 per square mile with its 56361 inhabitants and 2166086 square miles. It might be a cool place to perform social distancing.

We can observe that most of the features appear to be descriptive, except for the Other (%), which is mostly between 80 and 100. Due to the low variance, we will ignore it in our further analysis.

Populate the missing values

We are left with seven features that we are going to use to infer a similarity network between countries. One thing we need to do before that is to populate the missing values. We will use a simple method and fill in the missing values of the features with the average value of the region the country is part of.

UNWIND ["Arable (%)",
        "Crops (%)",
        "Infant mortality (per 1000 births)",
        "GDP ($ per capita)"] as feature
MATCH (c:Country)
WHERE c[feature] IS null
MATCH (c)-[:PART_OF]->(r:Region)<-[:PART_OF]-(other:Country)
WHERE other[feature] IS NOT null
WITH c,feature,avg(other[feature]) as avg_value
CALL apoc.create.setProperty(c, feature, avg_value) 
YIELD node
RETURN distinct 'missing values populated'

MinMax normalization

Last but not least, we have to normalize our features to prevent any single feature dominating over others due to a larger scale. We will use the simple MinMax method of normalization to rescale features between 0 and 1.

UNWIND ["Arable (%)",
        "Crops (%)",
        "Infant mortality (per 1000 births)",
        "GDP ($ per capita)",
        "Coastline (coast/area ratio)",
        "Pop. Density (per sq. mi.)",
        "Area (sq. mi.)"] as feature
MATCH (c:Country)
// Calculate the min and the max value for each feature
WITH max(c[feature]) as max,
     min(c[feature]) as min,
     feature
MATCH (c1:Country)
WITH c1,
    // define property name to store back results 
    "n_" + feature AS newKey,
    // normalize values
    (toFloat(c1[feature]) - min) / (max - min) as normalized_value// store results to properties
CALL apoc.create.setProperty(c1, newKey, normalized_value) 
YIELD node
RETURN distinct 'normalization done'

Similarity network with cosine similarity

We have finished the data preprocessing and can focus on the data analysis part. The first step of the analysis is to infer a similarity network with the help of the cosine similarity algorithm. We build a vector for each country based on the selected features and compare the cosine similarity between each pair of countries. If the similarity is above the predefined threshold, we store back the results in the form of a relationship between the pair of similar nodes. Defining an optimal threshold is a mix of art and science, and you’ll get better with practice. Ideally, you want to infer a sparse graph as community detection algorithms do not perform well on complete or densegraphs. In this example, we will use the similarityCutoff value of 0.8 (range between -1 and 1). Alongside the similarity threshold, we will also use the topK parameter to store only the top 10 similar neighbors. We do this to ensure a sparser graph.

MATCH (c:Country)// build the vector from features
WITH id(c) as id, [c["n_Arable (%)"],
                   c["n_Crops (%)"],
                   c["n_Infant mortality (per 1000 births)"],
                   c["n_GDP ($ per capita)"],
                   c["n_Coastline (coast/area ratio)"],
                   c["n_Pop. Density (per sq. mi.)"],
                   c["n_Area (sq. mi.)"]] as weights
WITH {item:id, weights: weights} as countryData
WITH collect(countryData) as data
CALL gds.alpha.similarity.cosine.write({
    nodeProjection: '*',
    relationshipProjection: '*',
    similarityCutoff:0.8,
    topK:10,
    data: data})
YIELD nodes, similarityPairs
RETURN nodes, similarityPairs

Graph data science library

With Neo4j’s Graph Data Science library, we can run more than 30 different graph algorithms directly in Neo4j. Algorithms are exposed as cypher procedures, similar to the APOC procedures we’ve seen above.

GDS uses a projection of the stored graph, that is entirely in-memory to achieve faster execution times. We can project a view of the stored graph utilizing the gdn.graph.create procedure. For more details on the GDS graph projection, check out my previous blog post. In this example, we will project nodes that have a label Country and relationships with a type SIMILAR.

CALL gds.graph.create('similarity_network','Country','SIMILAR');

Weakly connected components

More often than not, we start the graph analysis with the weakly connected components algorithm. It is a community detection algorithm used to find disconnected networks or islands within our graph. As we are only interested in the count of disconnected components, we can run the statsvariant of the algorithm.

CALL gds.wcc.stats('similarity_network')
YIELD componentCount, componentDistribution
RETURN componentCount, 
       componentDistribution.min as min,
       componentDistribution.max as max,
       componentDistribution.mean as mean,
       componentDistribution.p50 as p50,
       componentDistribution.p75 as p75,
       componentDistribution.p90 as p90

Results

The algorithm found only a single component within our graph. This is a favorable outcome as disconnected islands can skew the results of various other graph algorithms.

Louvain algorithm

Another community detection algorithm is the Louvain algorithm. In basic terms, densely connected nodes are more likely to form a community. It relies on the modularity optimization to extract communities. The modularity optimization is performed in two steps. The first step involves optimizing the modularity locally. In the second step, it aggregates nodes belonging to the same community into a single node and builds a new network from those aggregated nodes. These two steps are repeated iteratively until a maximum of modularity is attained. A subtle side effect of these iterations is that we can take a look at the community structure at the end of each iteration, hence the Louvain algorithm is regarded as a hierarchical community detection algorithm. To include hierarchical community results, we must set the includeIntermediateCommunitiesparameter value to true.

CALL gds.louvain.write('similarity_network',  
    {maxIterations:20,
     includeIntermediateCommunities:true,
     writeProperty:'louvain'})
YIELD ranLevels, communityCount,modularity,modularities

Results

We can observe by the ranLevels value that the Louvain algorithm found two levels of communities in our network. On the final level, it found eight groups. We can now examine the extracted communities of the last level and compare their feature averages.

MATCH (c:Country)
RETURN c.louvain[-1] as community,
       count(*) as community_size,
       avg(c['Arable (%)']) as pct_arable,
       avg(c['Crops (%)']) as pct_crops, 
       avg(c['Infant mortality (per 1000 births)']) as infant_mortality,
       avg(c['GDP ($ per capita)']) as gdp,
       avg(c['Coastline (coast/area ratio)']) as coastline,
       avg(c['Pop. Density (per sq. mi.)']) as population_density,
       avg(c['Area (sq. mi.)']) as area_size,
       collect(c['name'])[..3] as example_members
ORDER BY gdp DESC

Results

Louvain algorithm found eight distinct communities within the similarity network. The biggest group has 51 countries as members and has the largest average GDP at almost 22 thousand dollars. They are second in infant mortality and the coastline ratio but lead in population density by a large margin. There are two communities with an average GDP of around 20 thousand dollars, and then we can observe a steep drop to 7000 dollars in third place. With the decline in GDP, we can also find the rise of infant mortality almost linearly. Another fascinating insight is that most of the more impoverished communities have little to no coastline.

Find representatives of communities with PageRank

We can assess the top representatives of the final level communities with the PageRank algorithm. If we assume that each SIMILAR relationship is a vote of similarity between countries, the PageRank algorithm will assign the highest score to the most similar countries within the community. We will execute the PageRank algorithm for each community separately and consider only nodes and relationships within the given community. This can be easily achieved with cypher projection without any additional transformations.

WITH 'MATCH (c:Country) WHERE c.louvain[-1] = $community 
      RETURN id(c) as id' as nodeQuery,
     'MATCH (s:Country)-[:SIMILAR]->(t:Country) 
      RETURN id(s) as source, id(t) as target' as relQuery
MATCH (c:Country)
WITH distinct c.louvain[-1] as community, nodeQuery, relQuery
CALL gds.pageRank.stream({nodeQuery:nodeQuery,
                          relationshipQuery:relQuery, 
                          parameters:{community:community},
                          validateRelationships:False})
YIELD nodeId, score
WITH community, nodeId,score
ORDER BY score DESC
RETURN community, 
       collect(gds.util.asNode(nodeId).name)[..5] as top_5_representatives

Results

Network visualizations with Gephi

Excellent visualization is worth more than a thousand words. Gephi is a great tool to create network visualizations. As we might expect by now, APOC offers a handy procedure apoc.gephi.add that seamlessly streams network data from Neo4j to Gephi. Find out more in the documentation or in my previous blog post.

Node color indicates community, node size the GDP, and text size the community PageRank value

As we observed before, there are eight distinct communities in our network. The community with the highest average GDP is in the top right corner, and the countries with the highest to lowest average GDP follow in the clockwise direction. One intriguing triangle I found is right in the middle of the visualization formed by Russia, China, and Brazil. Also, if you look closely, you will see that Panama is part of the red community, but is positioned in the middle. That is because it has similar relationships to one or two countries from most of the communities, but is related to three countries from the red community, and hence belongs to it.

Hierarchical communities based on the Louvain algorithm

We mentioned before that the Louvain algorithm can be used to find hierarchical communities with the includeIntermediateCommunitiesparameter and that in our example, it found two levels of communities. We will now examine the groups of countries on the first level. A rule of thumb is that communities on a lower level will be more granular and smaller.

MATCH (c:Country)
RETURN c.louvain[0] as community,
       count(*) as community_size,
       avg(c['Arable (%)']) as pct_arable,
       avg(c['Crops (%)']) as pct_crops, 
       avg(c['Infant mortality (per 1000 births)']) as infant_mortality,
       avg(c['GDP ($ per capita)']) as gdp,
       avg(c['Coastline (coast/area ratio)']) as coastline,
       avg(c['Pop. Density (per sq. mi.)']) as population_density,
       avg(c['Area (sq. mi.)']) as area_size,
       collect(c['name'])[..3] as example_members
ORDER BY gdp DESC

Results

As expected, there are almost twice as many communities on the first level compared to the second and final level. An exciting community formed in second place by the average GDP. It contains only five countries, which are quite tiny as their average area size is only 364 square miles. On the other hand, they have a very high population density of around 10000 people per square mile. Example members are Macau, Monaco, and Hong Kong.

Graph exploration with Neo4j Bloom

Another excellent tool for network visualization with a higher focus on graph exploration is Neo4j Bloom. It provides the ability to customize the graph perspective and search queries, which can be used by people without any cypher query language skill to explore and search for insights within the graph. If you are interested to learn more, you can check this blog postwritten by William Lyon.

We will take a look at the countries of the final community with the highest GDP. It is a community of 51 countries, that has four distinct communities on the first hierarchical level.

Node color indicates first level community and node size indicates GDP

Before, we mentioned an exciting community of five tiny countries with an incredibly high population density. They are colored red in this visualization. The blue community has around 25% higher average GDP and almost half the infant mortality as the yellow one. On the other hand, the yellow community has on average more coastline than the blue one.

Conclusion

Neo4j ecosystem is well suited to perform and visualize network analysis. Graph Data Science library is a practical addition to the ecosystem that allows us to run various graph algorithms and perform graph analysis without much hassle. You can try it out either on your computer or you can create a Neo4j Sandbox account and get started within minutes.

As always, the code is available on GitHub.

Originally posted on Medium.com

Similar Posts: